|
| All HomeworkHomework 1| Points | Problem | Comment
|
|---|
| 5 | 1.1f | Be sure to list the rows in the standard order used in the textbook. |
Homework 2| Points | Problem | Hints
|
|---|
| 8 | 1.8 | One involves a true table and a few words. Another proof might begin with "Notice that it can only be false if..." and showing that it cannot happen.
| | 8 | 1.12 | Read each part carefully! |
Homework 3| Points | Problem | Comments
|
|---|
| 3 | 1.14 | It might help to rephrase it a bit.
| | 3 | 1.15c | Show your steps!
| | 5 | 1.16c | 3 points for translation, 2 points for true value
| | 3 | 1.17c | Clearly explain your answer.
| |
Homework 4| Points | Problem | Comments
|
|---|
| 6 | 1.20c | To be clear, express Problem 1.1.c in DNF. Show all of your work, including constructing the truth table. |
Homework 5| Points | Problem | Comments
|
|---|
| 9 | 3.5 | Be sure to fully justify your answers. |
Homework 6| Points | Problem | Comments
|
|---|
| 3 | 3.6 |
| | 4 | 3.8de | Don't forget to do both d and e!
| | 6 | 3.9def | Do d, e, and f! |
Homework 7| Points | Problem |
|
|---|
| 4 | 3.17 | You can assume f(x) is invertible.
| | 6 | 3.18 | Since we did not spend a lot of time proving things about 1-1 and onto, you should know that the proofs in this case are really simple, so do not overthink it. Carefully reread the definitions, and the information provided in the problem makes it pretty straightforward to prove or disprove each thing. |
Homework 8| Points | Problem |
|
|---|
| 6 | 4.19 | Use a pseudocode similar to the one in the book. |
Homework 9| Points | Problem | Comment
|
|---|
| 6 | 4.1 | Translate the various conditions into things like p, q, ¬p, etc. and apply the logic you learned in Chapter 1. Don't forget about DeMorgan's Law!
| | 6 | 4.3 | See previous comment. |
Homework 10
- (6 points) Given that there is a function pow(a,b)
that computes ab, write a function
int sumCubes(int n) that uses a for loop to compute
13+23+33+...+n3.
-
(3 points) Write a function boolean isSet(int n,int b)
that returns true if the bth bit of n is 1
and false otherwise. We order bits from right to left,
so isSet(n,0) determines whether or not n is odd or even.
It might help you to know that there is an operator a>>b that shifts
a to the right by b bits, discarding the low order bits.
For instance, 8 >> 2 gives you 2 and 15 >> 2 gives you 3.
Homework 11| Points | Problem |
|
|---|
| 6 | 4.10 | Make sure to take into account the cases where everyone is kicked out of a room and where only some people are kicked out of a room.
| | 4 | 4.15 a or b | For 4 points, do either (a) or (b), clearly stating which one! For 2 bonus points, do both, again clearly stating which is which.
| |
Homework 12| Points | Problem | Comments
|
|---|
| 5 | 5.4 | Show your work!
| | 5 | 5.5 | You do not have to prove it, but your work should clearly indicate how you arrived at your solution. |
Homework 13| Points | Problem | Comments
|
|---|
| 5 | 5.6 e | Notice: Just part e!
| | 5 | 5.16 | This one is actually fairly simple if you apply the formulas from the book and do a few steps of algebra. |
Homework 14| Points | Problem | Comments
|
|---|
| 5 | 5.6 b | There is an easy way and a hard way to do this one. Also, as always, show your work!
| | 5 | 5.6 h | You will need to know a few rules about logs to completely simplify this one, so be prepared to search for log formulas if you don't remember them. The solution to this is a very simple function!
| | 6 | 5.21 | For part (b), your algorithm should be a lot more efficient. |
Homework 15| Points | Problem | Comments
|
|---|
| 4 | 5.22 |
| | 4 | 5.31 | Plug in the values and matrices on the left and simplify it to get the 0 matrix. |
Homework 16| Points | Problem | Comments
|
|---|
| 5 | 5.37 | Start by letting X be the matrix with entries a, b, c, d in the 4 spots. The plug into the left and you will get a 2x2 matrix that is equal to the all ones matrix, which means you will have 4 equations with 4 unknowns. Plug them into each other to find a solution.
| | 5 | 5.39 | To be clear, you need to find a matrix A and a matrix B such that they matrices satisfy all 4 of the properties (not different examples for each of the 4 properties). |
Homework 17| Points | Problem | Comments
|
|---|
| 6 | 6.3 | Make sure to list them in increasing order and indicate when two grow at the same rate.
| | 4 | 6.4 a | Note: Just part (a)! This one should just be a few steps of algebra. |
Homework 18| Points | Problem | Comments
|
|---|
| 12 | 6.13 | Make sure you justify your answers! Also, in case you are unaware, the get method on an ArrayList takes Θ(1) time, but it takes Θ(n) time on a LinkedList. Indexing into an array (e.g. a[j]) also takes Θ(1) time. |
Homework 19| Points | Problem | Comments
|
|---|
| 5 | 7.1 | Make sure to include all of the required parts. |
Homework 20| Points | Problem | Comments
|
|---|
| 10 | 7.9 | You are trying to prove that the closed formula given in Example 7.82 is correct, using the fact that fn is defined recursively by fn = fn-1 + fn-2. Don't forget the base cases!The hint is telling you that 1+(1+√5)/2=[(1+√5)/2]2 and 1+(1-√5)/2=[(1-√5)/2]2. It's up to you to figure out why this is helpful. If you start doing the algebra, you should get to a step where that formula helps.
| |
Homework 21| Points | Problem | Comments/details
|
|---|
| 5 | 7.11c | Solve it using one technique. The next assignment will ask you to use 2 techniques!
| | 5 | that→ | Give a simple recursive algorithm int arraySum(int []a, int n) that computes the sum of all of the elements of an array of size n. You may not use a loop! |
Homework 22| Points | Problem | Comments/details
|
|---|
| 8 | 7.11c | (Redo!) Make sure to solve it using two different techniques!
| | 8 | 7.11e | Make sure to solve it using two different techniques! |
Homework 23| Points | Problem | Comments/details
|
|---|
| 6 | 8.4 | Read the problem carefully! |
Homework 24| Points | Problem | Comments/details
|
|---|
| 10 | 8.10 | Show your work!
| | 4 | 8.15 | This one might require some thought! Be sure to give a complete solution. |
Homework 25| Points | Problem | Comments/details
|
|---|
| 6 | 8.14 | Just interpret the notations, and do some algebra. Make sure tou show all of your work!
| | 6 | 8.33 | Do not forget to give the complexity of your algorithm. |
Homework 26| Points | Problem | Comments/details
|
|---|
| 6 | 8.19 | Think for a minute and this one is not too difficult. Make sure you justify your answer.
| | 6 | 8.22 | See the hint in the book! If you see the connection to the material in the textbook, this one should be fairly easy. |
Homework 27| Points | Problem | Comments/details
|
|---|
| 12 | 8.25 a, c, d, g | Read carefully! First, count the possibilities, and then determine how long it will take in each case. As suggested in the book, use meaningful units for each answer. |
Homework 28| Points | Problem | Comments/details
|
|---|
| 6 | 9.2 | Make sure you clearly explain your answer.
| | 6 | 9.3 | Hint: Label the vertices as in Example 9.42 and think about how to choose which vertices should go in each partite set based on the label (There is only one way to do it). Then look for patterns in the vertex labels of each partite set. |
Homework 29| Points | Problem | Comments/details
|
|---|
| 6 | 9.16 | Clearly justify your answer! |
Homework 30
- (8) Use Prim's algorithm to find a minimum spanning tree for the following graph.
Assume the adjacency lists are stored in numerical order and start from vertex 0. Give the value in the priority queue at every step of the algorithm (Look at Example 9.101). Draw the graph and darken the edges of the minimum spanning tree. (you may scan/photocopy that page from the book if you wish). Finally, give the weight of the minimum spanning tree.
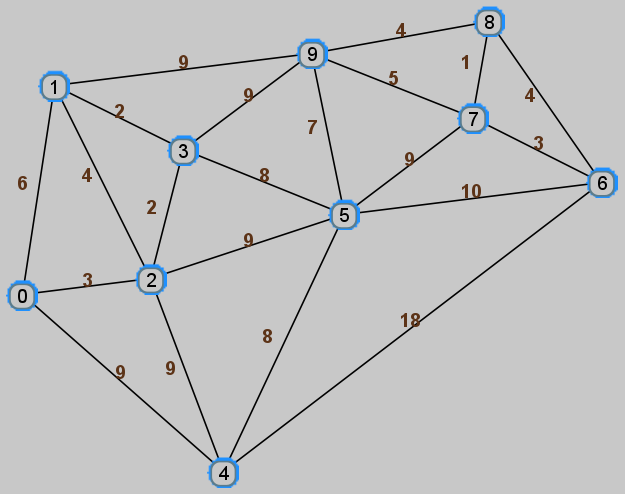
|
|
|