|
| Homework 15General Comments
- For full credit, provide context for each problem, show all calculations,
and justify all answers by providing enough comments to explain your reasoning.
- Homework assignments must be very neatly written or typeset
(e.g. using Word or OpenOffice).
- You can get up to 50% credit on a problem if you get significant outside assistance. Thus, if you are totally stuck on a problem it might be worth getting help. However, you must indicate any assistance/collaboration (See the Homework Assistance section on the Policies page). Failure to do so could result in a failing grade for the course! Note that getting help from the Help Center or me does not count as significant outside assistance, but talking with your classmates or searching on the Internet does!
- If a problem asks for an algorithm,
you should give the most efficient algorithm you can find to ensure full credit.
You should also specify the complexity of the algorithm with justification,
whether or not the problem asks for it.
Details
- (8) Use Floyd's algorithm to find the solution to the all-pairs shortest path
problem for this graph whose adjacency matrix is given here:
0 3 8 ∞ 1
∞ 0 ∞ 1 7
∞ 4 0 ∞ ∞
2 ∞ 2 0 ∞
∞ ∞ ∞ 6 0
-
(8) Use Prim's algorithm to find a minimum spanning tree for the following graph.
Assume the adjacency lists are stored in numerical order and start from vertex 0. Give the value in the priority queue at every step of the algorithm. Draw the graph and darken the edges of the minimum spanning tree. (you may scan/photocopy that page from the book if you wish). Finally, give the weight of the minimum spanning tree.
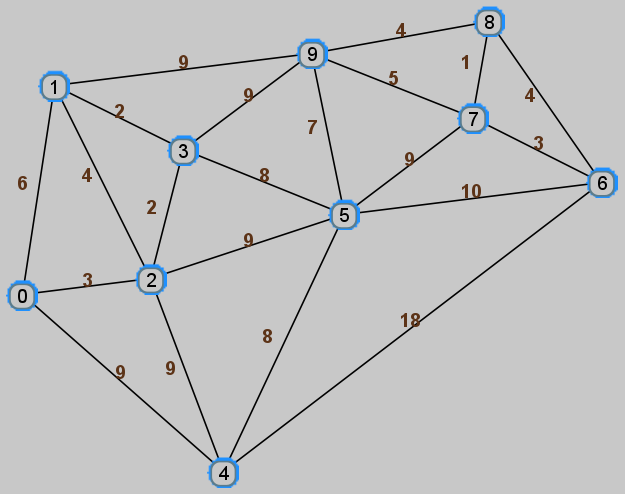
-
(8) Use Kruskal's algorithm to find a minimum spanning tree for the graph
in the previous problem.
Show the sets of vertices for every step of the algorithm. Draw the graph and darken the edges of the minimum spanning tree (you may scan/photocopy that page from the book if you wish). Finally, give the weight of the minimum spanning tree.
- (8) Construct a Huffman Encoding for the following data:
Symbol A B C D E F
Frequency 30 7 15 21 10 17
Give the encoding of each character and the total cost of encoding
a file containing these characters.
|
|
|