All Homework

Homework 1

An important skill to develop is implementing an abstract algorithm in an actual programming language. Thus, for this assignment you must implement one of the algorithms from the textbook to generate all permutations of the elements of an array.
Your program should be written in Java. Name your class CombinatoricsUtilities_Smith, where you should replace Smith with your last name. It should have a method
public static ArrayList⟨String[]⟩ generatePermutations(String[] input)
that returns an ArrayList of all permutations of the original array.
To help you debug your code, include a method public static void printList(ArrayList⟨String[]⟩) that prints each array in the ArrayList, one per line. Each array should be printed by printing each element with commas in between. E.g. For array ["blah","foo","bar"], the output should be
blah,foo,bar
Actually, add to the beginning of each line a number so it is easy to count the number of permutations. So the output should be numbered from 1 to n!. For instance, the output for a given permutation might look like:
3: blah,foo,bar
Implement a main method public static void main(String []args) that runs your algorithm on several lists, starting with lists of 3 elements, and including lists with 4, 5, and 8 elements.
Note: The easiest mistake to make with this algorithm is to not copy an array when you need to.
Submit your Java file(s) (NOT your .class files) using Webhandin 385-HW1.
Submit a brief write-up (Printed out) that includes a description of your algorithm and gives the computational complexity of it, with justification. (Convince me that you fully understand how the algorithm works and that you understand the analysis of it.)

Homework 2

(9) Complete the Convex Hull Assignment. You may work in pairs on this problem.
(1) After you have finished the first problem, complete the BRIDGES Survey, using the last 4 digits of your student number as your student ID code. Use "Convex Hull Assignment" for the name of the project. Your answers are confidential. Only one person has access to the data and it is not me. I will only receive summary data related to the class as a whole and an indication of whether or not you took the survey.

Homework 3

(6) Do problem 6.2.5 on page 216. Assume A' is upper-triangular and has been augmented with b' as its final column, and that it is indexed in the expected way (e.g. A'[i,j] is the entry in row i and column j). The solution should be placed in a vector x (e.g. x[1] will store the value of x₁, etc.)

Hint: Pay careful attention to how you solved systems with 3 or 4 variables. Which variable did you solve for first? How did you find each of the remaining variables? You should realize that the process you followed can be captured by a simple formula.

Do not forget to analyze your algorithm. (Hint: You will need to express it using one or more sums which you will then need to simplify.)
(4) Solve problem 6.6.11b on page 249 by reducing to a graph problem. Please do this problem on your own! I know that it is easy to find solutions for this one online, but you won't learn much by using one of those and you risk failing the assignment (unless you give credit, in which case the 1/2-credit policy applies).

Homework 4

(15) Consider a hash table of size 11, where the hash function h(k) = k mod 11 is used to determine the primary position of a key k in the table. You are tasked with inserting the following keys into the hash table:
Keys: 26, 12, 48, 36, 50, 37, 72, 92

For each collision resolution strategy below, show the state of the hash table after inserting all keys. Clearly indicate the sequence of steps for resolving collisions and provide the final table.
1. Use Open Hashing (Separate Chaining).
2. Use Closed Hashing with Linear Probing.
3. Use Closed Hashing with Double Hashing. Use the primary hash function h₁(k) = k mod 11 and the secondary hash function h₂(k) = 8 - (k mod 8). If a collision occurs at position i, resolve it by probing the next position using the formula:
```
i_next = (i + j · h₂(k)) mod 11
```
  where j is the number of attempts to resolve the collision. Do not forget that j starts back at 0 for every new insertion.
4. Compare and contrast how well each one performs.
(15) Given pattern needle and text heedlendlebadleednnnneeded, use each of the following search strategies to try to find the pattern in the text. For each, count the total number of comparisons and shifts made. Do not forget to give the shift table(s) for the appropriate algorithms.
1. Naive start at the beginning and shift by one after a failed match.
2. Horspool's Algorithm
3. Boyer-Moore Algorithm

Homework 5

(10) Solve the instance of the optimal binary search tree problem that contains items A, B, C, D, E, F with probabilities .15, .1, .23, .12, .33, .07 by using the algorithm from the textbook. Give the final tables and draw the tree. Show all of your work.
(10)
1. Ask chatGPT to solve Problem 1 for you. Include in your solution the question you asked and the entire response.
2. Evaluate chatGPT's solution. Did it get the correct solution? Did it explain it in a coherent way?
(10) Find a solution to the optimal binary search tree using items A-J with frequencies 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, 1/512 (assigned in that order). You may do it by hand, find help online, or use your intuition. In any of these cases, justify your solution. If you use chapGPT, you might want to double check to make sure it got it correct!
(20) Ask chatGPT for a Java implementation of an algorithm to solve the optimal binary search tree problem.
1. Look at it and see if you can figure out how the algorithm works (which might be easier if it gives you an algorithm similar to the one from our book). Evaluate whether or not you think it computes the correct solution.
2. Test the algorithm by running it on the textbook example (Not using ChatGPT. Copy-paste it into your favorite IDE), the example from Problems 1 and 3 above. Show the output of the algorithm! How did it do on these instances? Was it correct, close, or way off?
3. What is the efficiency of the algorithm? Is it more or less efficient than the algorithm given in the textbook?
4. Are there more efficient algorithms possible to solve this problem? Justify your answer. (Hint: Look at the exercises for section 8.3.)

Homework 6

(8 pts) IDAA 9.1.7 (page 323).
Prove that your algorithm is optimal.
Correct (4), complexity (2), optimal proof (2)
(6 pts) IDAA 9.3.3 (page 338).
Explain why the counterexample "breaks" the algorithm. Be specific. (2)
(6 pts) IDAA 9.3.6 (page 338)
Hint: See the book's hint!

Homework 7

(9) Complete the Huffman Encoding Assignment. You may work in pairs on this problem.
(1) After you have finished the first problem, complete the BRIDGES Survey, using the last 4 digits of your student number as your student ID code. Use "Convex Hull Assignment" for the name of the project. Your answers are confidential. Only one person has access to the data and it is not me. I will only receive summary data related to the class as a whole and an indication of whether or not you took the survey.

Homework 8

(9) Complete the Mountain Path Assignment. You may work in pairs on this problem.
(1) After you have finished the first problem, complete the BRIDGES Survey, using the last 4 digits of your student number as your student ID code. Use "Convex Hull Assignment" for the name of the project. Your answers are confidential. Only one person has access to the data and it is not me. I will only receive summary data related to the class as a whole and an indication of whether or not you took the survey.

Homework 9

(6+4+2 pts) Apply the Ford-Fulkerson algorithm to find the maximum flow of the following network.
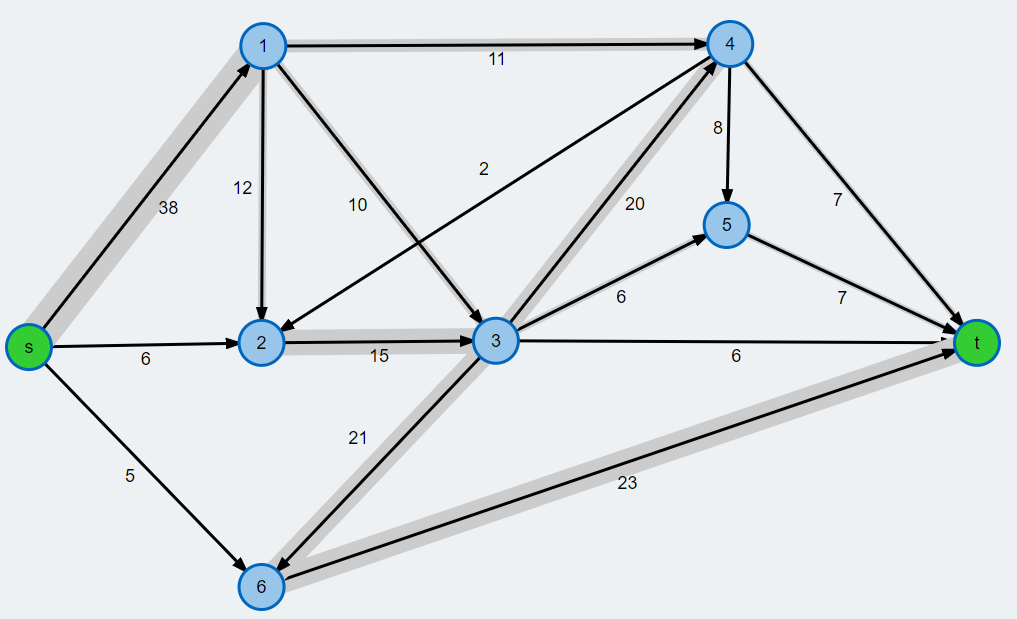Do not forget to:
1. Show all of the intermediate steps (copy this graph into your file and/or print it multiple times to make it easier!)
2. Draw the maximum flow and give the value of the maximum flow.
3. Specify the minimum cut (i.e. give the set X).
(6 pts) IDAA 10.2.10 (page 372).
Explain how to construct the appropriate graph and explain what a maximum flow tells us about the answer to the question.
Make sure you clearly explain your solution!
(6 pts) IDAA 10.3.1 (page 378)
Make sure to fully justify your answer.
(6 pts) IDAA 10.3.10 (page 380)
To clarify, it is looking for a tiling in which the lower left and upper right squares are empty, but the rest of the board is covered. Looking at a picture of a chess board might help. Make sure to prove your answer.

Homework 10

(12, 3 pts per part) IDAA 11.1.3 (page 393)
Part (b) is determining whether or not a graph is the complete graph (the wording is a little strange). Breifly justify your answers. Also, to show that the bound is tight, you need to give an algorithm that solves the problem in that much time.
(6 points) IDAA 11.1.7 (page 394)
Make sure your argument is very clear and complete.

Homework 11

(8 points) IDAA 11.3.7 (page 410)
Don't forget to (1) clearly state the decision version, (2) clearly outline the verification algorithm, and (3), justify that the verification algorithm is polynomial-time.
(5+2+2+3+2 pts) The Taylor Polynomial of degree n for computing eⁿ is given on page 412 (formula 11.6).
1. Use it to approximate the value of e^0.25≈1.28402541669... using a fifth-degree Taylor Polynomial (i.e. e^x≈1+x+...+x⁵/5! )
2. What is the absolute error of this approximation, to at least 10 decimal places?
3. What is the relative error of this approximation?
4. According to formula 11.8 on page 413, what is the maximum value of the expected absolute error?
5. Is the actual error greater than or less than the expected error? Explain why your answer makes sense.

Homework 12

Implement QuickSort_MINE, ParallelQuickSort_MINE, and FJQUickSort_MINE in the Eclipse project on Loki (I have already copied the code into your accounts).

Important Notes

You may work in pairs on this assignment if you wish.
You may help each other with using Java ForkJoin.
Other than me or classmates, do not seek outside help for QuickSort_MINE.java and/or ParallelQuickSort_MINE.java (e.g. AI, StackOverflow, etc.). This part should be pretty straightfoward.
You may use outside help to assist with implementing FJQuickSort_MINE, but your goal should be to understand the algorithm, not just implement it. This includes ChatGPT, etc. In order to optimize it, you will definitely need to understand it.
A warning: I had ChatGPT help me with my version of FJQuickSort_MINE and the first version was terrible--it wasn't really parallel. Then it wasn't correct and I spent a few hours tracking down the problem. Then the overall algorithm was parallel, but it didn't make partitionUp and partitionDown parallel. In all, with ChatGPT's help and a lot of looking deeply at the code, I spent several hours getting a working version.
I had to override the public void sort(int[] array) method because I needed to use a second array and there isn't a nice way to do it without instantiating the array and an addition boolean variable I needed. You cannot do it in compute() because that gets called numerous times and would result in multuple copies of the second array. So my version of sort has all of the original code from the superclass, but with two new lines before the call to pool.invoke(this).
I have been having a hard time consistently copy/pasting from Eclipse running on Loki to my desktop and I do not know if I have a wonky mouse or it has something to do with the clipboard between the two. Just a warning that you may or may not experience the same. If you have a hard time as well, create a textfile in your Eclipse project and you should be able to paste it into there.

Details

Get a Windows machine.
Download MobaXterm (the CS laptops should have it).
Create an SSH profile for loki.cs.hope.edu.
Make sure you go to Advanced SSH settings and check "X11-Forwarding" if it is not already checked.
You may need to be on campus to access Loki. If you have problems and you are on campus, contact me right away with specific details. There may be a firewall setup that I forgot about.
Log in to Loki using your 1Hope username and your student ID as your password (including the leading 0s).
On the command line, type eclipse and press Enter.
Wait a minute and Eclipse should pop up on your computer. Note that it is actually running on Loki, but the GUI is on your machine.
On the first screen, just click Launch and accept the default workspace.
Click the Hide icon on the top right.
Click File → Import → General → Existing Projects into Workspace.
Click Next.
Click Browse, select Java_Parallel_Sorts and click Open.
Click Finish.
Navigate to src → sorts → RunSortsFromFile.java and open it.
Right-click it and select Run as → Java Application.
It should start running but print "****Sort incorrect: Quicksort_MINE" and quit since you haven't implemented it yet.
To make sure you have enough memory, right-click on RunSortsFromFile, select Run as → Run Configurations..., Click the Arguments tab, and under the VM Arguments add:
```
-Xms8096m
-Xmx32768m
```
Implement your best Quicksort in QuickSort_MINE.java and run tests 0 and 1.
When you have a good implementation of QuickSort, implement ParallellQuickSort_MINE. This should be the naive parallel algorithm that uses normal partition but parallel recursive calls to QuickSort.
Uncomment line 58 ("ParallelQuickSort_Mine",).
Run RunSortsFromFile with tests 0 through 3 and try to optimize your implementation by setting cutoffs at different values. There are two types of cutoffs—
- the insertionSort cutoff where QuickSort calls that instead of QuickSort for small arrays (you decide what small is), and
- the sequential cutoff where you stop making new threads and just call the regular sequential version of QuickSort.
If it is taking a really long time on 0–2 (more than 30 minutes), or crashing, make sure you have been clever about repeated elements. This is a subtle problem, but if you do not solve it, you will not get very far into the tests.
Next implement FJQuickSort_MINE, uncomment line 59 ("FJQuickSort_Mine",) and run the tests again, this time including 0–3. Optimize this by playing with the cutoffs.

Helpful code
I should have given you this sooner, but these might be helpful:


    /**
     * Inner class to represent a range [lo, hi) (hi exclusive).
     */
    private static class Range { // looks good
        int lo, hi;
        Range(int lo, int hi) { this.lo = lo; this.hi = hi; }
    }

    /**
     * Inner class corresponding to the pnode structure.
     * Represents a segment of the array and holds counts.
     */
    private static class PNode { // looks good.
        PNode left, right;
        int sum, sum2;  // Counts: sum = # of values < pivot, sum2 = # of values > pivot.
        int lo, hi;     // Interval [lo, hi) (hi exclusive)
        int fl, fl2;    // Prefix sums (fromLeft values)
        PNode(int lo, int hi) {
            this.lo = lo; this.hi = hi;
            left = right = null;
            sum = sum2 = fl = fl2 = 0;
        }
    }

Submitting:

On the first due date:
- Submit QuickSort_MINE.java, ParallelQuickSort_MINE.java, and any other Java files you created by copying them into your shared folder.
- Put a Google Doc in your shared folder and put the results of tests 0, 1, and 2 in it.
On the second due date:
- Submit QuickSort_MINE.java, ParallelQuickSort_MINE.java, FJQuickSort_MINE.java, and any other Java files you created by copying them into your shared folder.
- Put a Google Doc in your shared folder and put the results of tests 0, 1, and 2, and 3 in it.
On the third due date:
- Bring a printout to class of your writeup--the details are below.

Write Up
Give thoughtful answers to the following questions and submit a hardcopy in class. Please take the write-up seriously and don't just throw it together at the last minute.

Give a brief description of your algorithms. Focus on how you parallelized each. Explain in detail what was parallelized and how, and what was not. Use words like divide-and-conquer, prefix, pack, tree, etc. as appropriate.
Give a tight bound on the expected running time of both of your parallel algorithms assuming you had k cores. Give both the work and span. Make sure you justify your analysis. Hint: It may not be exactly what you expect it to be!
When you compute speedup of the parallel algorithms, should you compare to your Quicksort or the Java Quicksort? Explain why. (There is a correct answer to this question!)
Compute the speedup of both parallel algorithms based on the summary of the results.
Discuss the performance/speedup of the parallel algorithms, comparing the actual speedup of each with the expected ideal speedup.
Compare the two parallel implementations with each other. Which did you expect to be better? Which one was actually better? Try to explain the results.
Discuss any limitations of your parallel algorithms. What is the limiting factor of how much you can parallelize it? Could it be made faster? If so, explain.
If one or both algorithms did not perform as well as you expected, what do you think were the reasons? Be as specific as possible.
Grade yourself out of 20 points, providing a clear justification. Take into account how well you did in your implementations of the parallel algorithms and how well you did in answering the questions in the write up.

My Results
Here are my latest results after just a little bit of fine tuning. Hopefully you can match or beat my performance.

Running on Loki (24 cores)

-------------------------------------------------------------
Running tests from file: tests_large.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:       503002   0.203394   0.088787   0.024670   0.267465 
r:      1250001   0.092884   0.150121   0.030659   0.045087 
r:      2250001   0.170563   0.299640   0.078282   0.053893 
r:      4250001   0.335288   0.607453   0.176322   0.107004 
r:     10250001   0.856752   1.563091   0.279726   0.232635 
r:     20250001   1.827221   3.196473   0.508888   0.368734 
r:     40250001   3.655460   6.575102   0.832063   0.821372 
i:      1004321   0.001744   0.038280   0.003473   0.006927 
i:      2004321   0.072241   0.104963   0.012542   0.022034 
i:      4004321   0.113611   0.107130   0.012732   0.027865 
o:      1111111   0.005895   0.045190   0.009523   0.008220 
o:      2111111   0.049569   0.100849   0.016917   0.015217 
o:      4111111   0.088278   0.218459   0.034993   0.032281 
o:      8111111   0.299145   0.509163   0.098337   0.099883 
o:     16211511   0.345972   0.742189   0.136868   0.137849 
m:       100004   0.003722   0.007084   0.002135   0.003694 
m:       100500   0.004625   0.006994   0.003249   0.003740 
m:       100080   0.005814   0.010063   0.002902   0.004449 
m:       100300   0.009384   0.015604   0.004164   0.005544 
m:      1000081   0.075003   0.151719   0.026143   0.022880 
m:      2000081   0.141099   0.276027   0.063283   0.040544 
m:      4000081   0.274243   0.532726   0.096853   0.066980 
m:      8000081   0.519874   0.999514   0.211910   0.150669 
c:       100070   0.006056   0.024731   0.003828   0.005555 
c:      1040500   0.074378   0.172998   0.033168   0.028030 
c:      2040500   0.155635   0.311727   0.078199   0.044131 
c:      4040500   0.320199   0.606346   0.116547   0.080554 
c:      8040500   0.670086   1.204830   0.209200   0.152496 
R:       100070   0.006400   0.016883   0.003353   0.007387 
R:      1040500   0.073910   0.175591   0.029750   0.025610 
R:      2040500   0.145363   0.283206   0.075018   0.045178 
R:      4040500   0.313946   0.604893   0.097593   0.074682 
R:      8040500   0.660016   1.176030   0.238098   0.159616 
Average Times (s):
Java S     :     0.3508 s
QS Mine    :     0.6341 s
PQS Mine   :     0.1076 s
FJQS Mine  :     0.0960 s

Total time   0.736085 minutes
-------------------------------------------------------------
Running tests from file: tests_reallyLarge.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:     10000000   1.228781   1.405497   0.188801   0.766923 
r:     20000000   2.033788   2.956669   0.530801   0.393491 
r:     40000000   4.276630   6.348801   0.865244   0.772575 
r:     80000000   8.980686  12.999945   1.699632   1.625627 
i:     10000000   0.367616   0.237449   0.029648   0.090409 
i:     20000000   0.865593   0.562999   0.080425   0.370541 
i:     40000000   1.246394   0.901323   0.091485   0.330381 
i:     80000000   2.710100   1.935311   0.183992   0.681789 
o:     10000000   0.358633   0.528750   0.082653   0.088299 
o:     20000000   0.557833   0.854979   0.168250   0.159289 
o:     40000000   1.102360   1.846913   0.321904   0.323383 
o:     80000000   2.234918   3.793348   0.556909   0.694399 
m:     80000000   5.916277   9.025665   1.653428   1.228704 
c:     80000000   8.887554  13.020015   1.745730   1.504531 
R:     80000000   8.791967  12.971047   1.783740   1.577811 
Average Times (s):
Java S     :     3.3039 s
QS Mine    :     4.6259 s
PQS Mine   :     0.6655 s
FJQS Mine  :     0.7072 s

Total time   2.705603 minutes
-------------------------------------------------------------
Running tests from file: tests_huge.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:    320000000  34.638313  55.393139   6.528632   6.318784 
r:    640000000  70.554837 115.153457  12.883820  16.742646 
i:    320000000   7.415055   8.752327   0.820084   2.506834 
i:    640000000  20.334999  17.156517   1.616368   6.531858 
o:    320000000   8.988480  16.394475   2.293333   3.316840 
o:    640000000  13.947722  30.372730   4.238275   6.708544 
m:    320000000  24.572505  43.428682   6.064091   6.175202 
m:    640000000  60.706583 102.047471  11.832715  14.782534 
c:    320000000  33.640449  56.306590   5.492318   6.771770 
c:    640000000  69.872350 114.180984  12.254811  13.462848 
R:    320000000  33.340344  56.306715   5.663436   5.783646 
R:    640000000  70.223275 117.525818  11.762168  13.605198 
Average Times (s):
Java S     :    37.3529 s
QS Mine    :    61.0849 s
PQS Mine   :     6.7875 s
FJQS Mine  :     8.5589 s

Total time  26.908848 minutes
-------------------------------------------------------------
Running tests from file: tests_reallyHuge.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:    640000000  66.924306 117.355123  13.599491  16.321587 
r:   1280000000 139.624436 243.188431  25.998576  28.552879 
i:    640000000  19.101756  18.730480   1.468419   6.357497 
i:   1280000000  23.944650  36.019101   2.566010  11.615234 
o:    640000000  14.054652  33.987900   4.404676   5.673978 
o:   1280000000  23.271441  64.610262   8.525141  12.142073 
m:    640000000  58.768287 102.604546  11.836725  12.037366 
m:   1280000000  96.353756 177.318966  21.438138  21.382085 
c:    640000000  67.157148 115.262043  13.027712  14.170147 
c:   1280000000 139.844418 244.632203  24.479397  24.718680 
R:    640000000  67.680449 118.589893  12.810518  11.116423 
R:   1280000000 141.452009 250.166631  27.495656  33.195717 
Average Times (s):
Java S     :    71.5148 s
QS Mine    :   126.8721 s
PQS Mine   :    13.9709 s
FJQS Mine  :    16.4403 s

Total time  54.952003 minutes
-------------------------------------------------------------

Running on my Lenovo laptop. 4 cores, 8 logical processors.

-----------------------------------------------------------
Running tests from file: tests_large.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:       503002   0.196056   0.110415   0.017088   0.054035 
r:      1250001   0.108144   0.162833   0.037057   0.037386 
r:      2250001   0.194447   0.303849   0.070569   0.074659 
r:      4250001   0.391241   0.587288   0.122643   0.175339 
r:     10250001   0.997115   1.522100   0.338254   0.342308 
r:     20250001   2.025844   3.287349   0.681092   0.726915 
r:     40250001   4.091287   7.041757   1.441059   1.644955 
i:      1004321   0.002119   0.023440   0.005228   0.012317 
i:      2004321   0.116661   0.077668   0.018173   0.031347 
i:      4004321   0.152022   0.095759   0.021145   0.056583 
o:      1111111   0.008538   0.033952   0.011787   0.013391 
o:      2111111   0.087724   0.090357   0.028515   0.026970 
o:      4111111   0.121594   0.188058   0.051983   0.055546 
o:      8111111   0.489528   0.894020   0.184089   0.206916 
o:     16211511   0.616131   0.944212   0.235521   0.234058 
m:       100004   0.004615   0.007282   0.002466   0.002725 
m:       100500   0.005270   0.007405   0.002579   0.002730 
m:       100080   0.007006   0.010285   0.003222   0.003393 
m:       100300   0.007223   0.011368   0.003380   0.004155 
m:      1000081   0.091678   0.136657   0.026776   0.029215 
m:      2000081   0.174453   0.266360   0.063249   0.066448 
m:      4000081   0.442076   0.662866   0.181968   0.124749 
m:      8000081   0.742841   1.102124   0.253777   0.251919 
c:       100070   0.009120   0.014784   0.003580   0.003686 
c:      1040500   0.119476   0.155761   0.036451   0.033431 
c:      2040500   0.216432   0.373375   0.082641   0.062868 
c:      4040500   0.441212   0.694685   0.146030   0.128814 
c:      8040500   0.814874   1.237456   0.246835   0.265993 
R:       100070   0.007706   0.011651   0.003576   0.004268 
R:      1040500   0.111485   0.178281   0.036593   0.032261 
R:      2040500   0.227520   0.369837   0.079266   0.168331 
R:      4040500   0.488805   0.727092   0.135376   0.120916 
R:      8040500   0.929683   1.416562   0.298969   0.225666 
Average Times (s):
Java S     :     0.4376 s
QS Mine    :     0.6893 s
PQS Mine   :     0.1476 s
FJQS Mine  :     0.1583 s

Total time   0.895700 minutes
-----------------------------------------------------------
Running tests from file: tests_reallyLarge.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:     10000000   1.162170   1.409333   0.273885   0.443067 
r:     20000000   1.864027   3.005923   0.599462   0.654189 
r:     40000000   3.717655   6.580540   1.448707   1.587761 
r:     80000000   8.574365  15.668847   3.185012   3.401737 
i:     10000000   0.343006   0.310538   0.079732   0.195487 
i:     20000000   0.819757   0.791059   0.223463   0.556002 
i:     40000000   1.797632   1.424420   0.388915   0.568846 
i:     80000000   2.613558   2.372171   0.632129   1.169147 
o:     10000000   0.413366   0.545427   0.149457   0.143715 
o:     20000000   0.567881   1.147562   0.346725   0.250001 
o:     40000000   1.078251   2.120411   0.689249   0.621208 
o:     80000000   2.160659   4.299791   1.332958   1.448592 
m:     80000000   6.510522  10.878236   2.241679   2.185895 
c:     80000000   9.178449  14.566119   3.388897   3.267340 
R:     80000000  11.306799  16.183571   3.315677   3.468758 
Average Times (s):
Java S     :     3.4739 s
QS Mine    :     5.4203 s
PQS Mine   :     1.2197 s
FJQS Mine  :     1.3308 s

Total time   3.414294 minutes
-----------------------------------------------------------
Running tests from file: tests_huge.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:    320000000  37.084305  64.132488  15.084456  16.906848 
r:    640000000  76.078501 129.333295  25.318910  43.409221 
i:    320000000   9.515072   9.465067   1.991441   4.949963 
i:    640000000  22.833383  20.339464   4.215962  11.138592 
o:    320000000  10.993523  20.189892   4.778598   5.056805 
o:    640000000  18.750882  39.416145  13.364968  22.677691 
m:    320000000  28.132583  49.617576  10.354699  11.501614 
m:    640000000  68.073984 112.594090  21.630860  33.308942 
c:    320000000  41.071430  74.173983  12.829930  14.859091 
c:    640000000  72.217650 122.996195  23.447898  36.977432 
R:    320000000  36.072326  58.660940  11.433255  12.842222 
R:    640000000  72.477797 119.756850  23.670875  34.227131 
Average Times (s):
Java S     :    41.1085 s
QS Mine    :    68.3897 s
PQS Mine   :    14.0102 s
FJQS Mine  :    20.6546 s

Total time  34.999238 minutes
-----------------------------------------------------------
Running tests from file: tests_reallyHuge.txt
           size     Java S    QS Mine   PQS Mine  FJQS Mine 
r:    320000000  34.928797  59.904938  12.266449  16.057059 
r:    640000000  71.667810 127.179825  22.905939  38.343888 
r:   1280000000 150.412458 256.613579  49.776536  75.869430 
i:    320000000   9.239585   9.840005   1.863642   8.201292 
i:    640000000  22.041937  21.699923   4.253902  10.827467 
i:   1280000000  30.442981  42.191836   8.828616  25.701493 
o:    320000000  12.112377  20.089179   4.491200   8.571819 
o:    640000000  18.740276  37.930484   8.729651  10.756061 
o:   1280000000  32.415053  88.847442  21.513413  36.728646 
m:    320000000  25.475168  45.829511   8.694908  13.470144 
m:    640000000  62.466809 108.081626  22.938140  27.809189 
m:   1280000000 106.988573 192.455194  43.845626  53.152297 
c:    320000000  34.566493  63.019025  12.545652  17.400979 
c:    640000000  70.779691 120.906311  26.060827  30.940941 
c:   1280000000 145.689857 251.720583  54.912333  80.140976 
R:    320000000  34.071229  57.169652  11.841701  13.849037 
R:    640000000  68.273679 125.556167  24.594034  35.532317 
R:   1280000000 144.450273 250.380874  54.500816  77.958457 
Average Times (s):
Java S               :      59.71 s
QS Mine              :     104.41 s
PQS Mine             :      21.92 s
FJQS Mine            :      32.30 s

Total time  98.399966 minutes
-----------------------------------------------------------

Homework 13

You may work in pairs on this assignment.

The following are from Grossman Homework. They will be equally weighted (10 points each).

Write a program for Problem 1 but with some modifications— Keep reading!.

Start with the code at LongestSequence for code to get you started and a decent test program. Please rename your class LongestSequence_Smith, where Smith is your last name, and make sure to change it in the test program.

The code on page 27 of the Grossman notes is a good starting point.

If you can figure out how, run it on Loki so you can test it with 24 cores.
Submit your results as a textfile or on paper.
For a lot of helpful tips on implementing your algorithm using ForkJoin, see Beginner's Introduction to Java's ForkJoin Framework and/or examples from the book.
Hand in your code by placing it in the same shared directory as usual.
Do Problem 3. Use Excel or a similar program to create the tables of values and charts. Submit your Excel file by putting it in your shared folder. If you use another program make sure you submit a printed copy of your tables and charts.
Do Problem 4. Hand this one in on paper.