CSCI 255 Fall 2024
Introduction to Algorithms and Discrete Structures		Archived Class
Charles Cusack
Computer Science
Hope College
Main
Schedule
Grading
Gradebook
Homework
Policies
Advice
College
    Policies
Notes
Programs
Tutorials
CSCI 125
CSCI 255
Others
Admin

Homework 11

General Comments

  • For full credit, provide context for each problem, show all calculations, and justify all answers by providing enough comments to explain your reasoning.
  • Homework assignments must be very neatly written or typeset (e.g. using Word or OpenOffice).
  • You can get up to 50% credit on a problem if you get significant outside assistance. Thus, if you are totally stuck on a problem it might be worth getting help. However, you must indicate any assistance/collaboration (See the Homework Assistance section on the Policies page). Failure to do so could result in a failing grade for the course! Note that getting help from the Help Center or me does not count as significant outside assistance, but talking with your classmates or searching on the Internet does!
  • If a problem asks for an algorithm, you should give the most efficient algorithm you can find to ensure full credit. You should also specify the complexity of the algorithm with justification, whether or not the problem asks for it.

Details

  1. (8) Complete the Kevin Bacon Assignment. You may work in pairs on this problem, but not on the rest of the assignment.
  2. (1) After you have finished the first problem, complete the BRIDGES Survey, using the last 4 digits of your student number as your student ID code. Your answers are confidential. Only one person has access to the data and it is not me. I will only receive summary data related to the class as a whole and an indication of whether or not you took the survey.
  3. Consider the following directed acyclic graph.
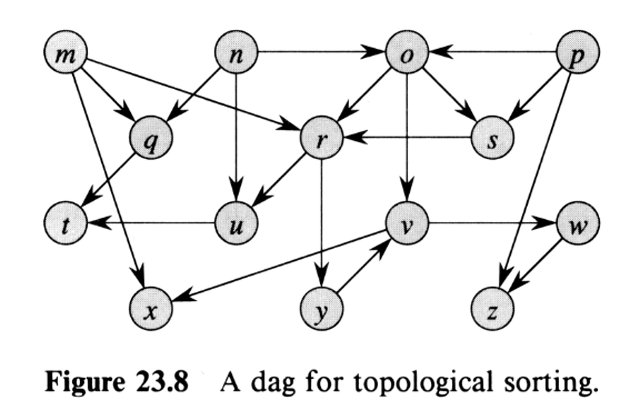
    1. (8) Find a valid topological sorting of the DAG using the DFS algorithm from the lecture notes (not from the book). Show all of your work, including the timestamps! (Print/copy/redraw the graph and write the timestamps on the nodes.) Do not forget to give the final topological ordering!
    2. (8) Find a valid topological sorting of the DAG using the source-removal algorithm from the book. Clearly indicate the order in which the states are removed! (Best done by copying/printing/redrawing the graph and numbering the nodes in the order they are removed.) Do not forget to give the final topological ordering!
  4. (8) Design a decrease-by-half algorithm that computes ⌊log2 n⌋. Do not forget to give the work case complexity!
    Note: Do not look up an algorithm. Come up with your own!
  5. (Bonus 4) You are given an n×n matrix whose rows and columns are sorted in increasing order. Design a O(n) algorithm to find a given number in the matrix. Make sure you justify the complexity of the algorithm. Also, make sure you understand the properties the matrix has—do not assume too much or too little! This one is a bit tricky, so it may take you some time and experimentation to find a good algorithm.