|
| All HomeworkHomework 1
- AIDMA Problem 2.1
- AIDMA Problem 2.4 (Note: You just need to rephrase the statement, not prove anything!)
Homework 2
- AIDMA Problem 2.12
- AIDMA Problem 2.19
- AIDMA Problem 2.22
- AIDMA Problem 2.23
Homework 3
- AIDMA Problem 3.3 b
- AIDMA Problem 3.12
Homework 4
- Rank the following functions in increasing order of growth rate.
- \(7n\log n\)
- \(n^3 + 100n^2\)
- \(2^{\sqrt{n}}\)
- \(n + 5\)
- \((\log n)^2 + 3\)
- \(n!\)
- \(n^{3/2} - 100n\)
- \(3^{n}\)
- \(\sqrt{n} + \log n\)
- \(42\)
- \(n^2\log n + 50n^2\)
- \(5n^2\)
- \(0.5n\log n\)
- \(2^{n} - n^{10}\)
- \(\log\log n + 20\)
-
Let \( f(n) = 5n^3 + 2n^2 + 7 \).
Prove that
\( f(n) = \Theta(n^3) \):
-
Using the definition.
-
Using the Limit Theorem.
Homework 5Analyze Best and Worst Case Running Times
Give tight bounds for the best and worst case running times of each algorithm
in terms of input size. Unless noted, assume A.length = n. Do not worry about what the code does;
only analyze how long it takes. Use standard asymptotic notation and justify briefly on your own.
-
Early exit on a sentinel value.
int scanUntilZero(int[] A) {
int s = 0;
for (int i = 0; i < A.length; i++) {
s += A[i];
if (A[i] == 0) break;
}
return s;
}
-
Nested search over the prefix. Early exit on first duplicate.
int hasDuplicatePrefix(int[] A) {
for (int i = 0; i < A.length; i++) {
for (int j = 0; j < i; j++) {
if (A[i] == A[j]) return 1;
}
}
return 0;
}
-
Pair counting with a break depending on a threshold \(S\).
void countPairsUpToS(int[] A, int S) {
int c = 0;
for (int i = 0; i < A.length; i++) {
for (int j = i + 1; j < A.length; j++) {
c++;
if (A[i] + A[j] > S) break;
}
}
}
-
Divide by 2 until zero.
void halfWhile(int n) {
while (n > 0) {
n = n / 2;
}
}
- Tricky one!
void sqrtStepper(int n) {
for (int i = 1; i * i <= n; i++) {
// O(1) work
}
}
-
Changing inner loop.
void doublingInner(int n) {
for (int i = 1; i <= n; i++) {
int k = 1;
while (k < i) {
k = k * 2;
}
}
}
-
Triangular nested loop with a possible early break based on a changing accumulator.
void triangularPlusBreak(int n) {
int t = 0;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
t += i + j;
if (t % 1000 == 0) break;
}
}
}
-
Fixed-size inner loop of constant \(M\) iterations.
int fixedInnerConstant(int[] A) {
int M = 250; // constant
int s = 0;
for (int i = 0; i < A.length; i++) {
for (int j = 0; j < M; j++) {
s += A[i] + j;
}
}
return s;
}
-
Two separate parameters: total work depends on both \(n\) and \(m\).
void twoParameters(int n, int m) {
int x = 0;
for (int i = 0; i < n; i++) x++;
for (int j = 0; j < m; j++) x++;
}
-
Fully nested two-parameter loops.
void nestedTwoParameters(int n, int m) {
long x = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
x += i + j;
}
}
}
-
Three nested loops with possible immediate return.
void threeNestedWithBreak(int n) {
long x = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
for (int k = 0; k < j; k++) {
x++;
if (x == 5) return;
}
}
}
}
-
Mixed for/while.
void mixedForWhile(int n) {
int count = 0;
for (int i = 1; i <= n; i++) {
int t = i;
while (t > 0) {
t = t / 3;
count++;
}
}
}
-
Early exit when a running sum exceeds a threshold; otherwise full scan.
int sumWithSentinel(int[] A) {
int s = 0;
for (int i = 0; i < A.length; i++) {
s += A[i];
if (s > 1000000) return s;
}
return s;
}
-
Work per iteration grows with the index: total work is the sum.
void variableWorkPerIter(int n) {
for (int i = 1; i <= n; i++) {
for (int t = 0; t < i; t++) {
// 1 step per t
}
}
}
Homework 6-
(10) Do the Sorting Comparison Assignment.
You may work in pairs on this assignment.
Homework 7
-
Max Solvable Input Size: Assume your algorithm for Subeset Sum runs in \( 5n \cdot 2^n \) steps and your machine processes 100 million steps/second. Estimate the largest value of \( n \) solvable in 1 second, 1 minute, 1 hour, 1 day, 1 month, 1 year, 100 years, and 1000 years. Show your work. (Hint: You might want to use a spreadsheet to help you with the calculations. If so, make sure what you submit has enough details printed so I can determine the formulas.)
- Subarray Sum Match:
Given an array of positive integers \( A[0 \dots n-1] \) and an integer target value \( k \), find all contiguous subarrays whose elements sum to exactly \( k \). (A contiguous subarray is a subset consisting of all of the
elements from some index \(i\) to some index \(j\geq i\).)
- Design and write a brute-force algorithm using a nested loop to solve this problem.
- What are the best-case and worst-case time complexities?
- Apply your algorithm to the example \( A = [1, 5, 2, 7, 4, 2, 5] \) with \( k = 10 \). Show all subarrays considered.
Homework 8
-
(8) Complete the
Kevin Bacon Assignment.
You may work in pairs on this problem,
but not on the rest of the assignment.
-
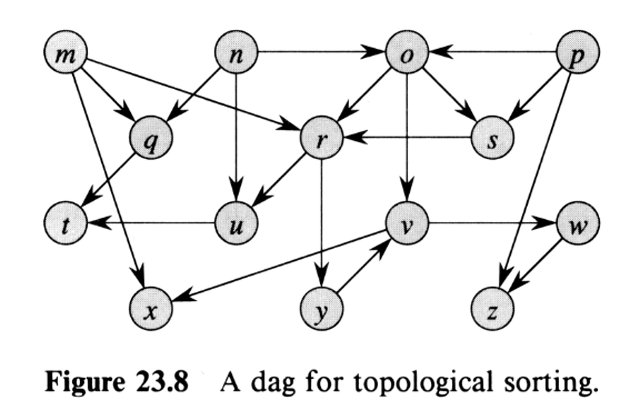
(6) Run DFS on the following DAG.
Process the vertices in alphabetical order, both in the overall
algorithm and the adjacency lists!
Print/copy/redraw the graph and write the timestamps on the nodes.
- Show the discovery and finishing timestamps for every vertex.
- Classify every edge (tree, back, forward, cross).
- List the vertices in decreasing order of their finishing times (largest finish time first).
In fact, redraw the graph with the vertices lined up in that order.
- Observation: What special property does the ordering from part (c) have for a DAG? State it in one sentence and explain why it holds using the DFS timestamps.
- (6) Problem 10 from BFS (Even-Length Cycle Detection via BFS).
Homework 9
-
Let \(T(n)\) be defined by \(T(1)=1\) and
\(T(n) \;=\; 4\,T\!\left(\frac{n}{3}\right) + n\),
where \(n = 3^k\), for \(k=0,1,2,\ldots\)
For this assignment, you will show that the
solution to this recurrence relation is
- \(T(n)=4\,n^{\log_3 4}-3n\), or
- \(T(3^k)=4^{\,k+1}-3^{\,k+1}\), or
- \(T(n)=\Theta(n^{\log_3 4})\),
where the first two formulas are equivalent, one expressed in terms
of \(n\) and the other in terms of \(k\)
(Remember, we are assuming \(n = 3^k\)), and the third is a bound.
For each of the following, choose the form of the answer that is easiest to
work with for that given proof type.
-
Prove the given result using Iteration (also called backward substitution).
- Prove the given result using Substitution (prove it by induction).
- Prove the given result using the Master Theorem.
Homework 10
- (10) Homework Problem 5 from Strassen's Algorithm (Hands-on Strassen multiplying 4x4 matrices.)
- (10) Homework Problem 6 from Divide-and-Conquer (Weight Calibration).
Homework 11
-
(10) Complete the
Convex Hull Assignment.
You may work in pairs on this problem.
Homework 12
- Problem 3 (Recursive Digit Sum) from Decrease-by-a-Constant Homework Problems
-
Problem 7 (Interpolation-Based Search) from Binary Search Homework Problems
Homework 13Details coming!
- (13) Do the City Distances BRIDGES assignment.
Submit the code via you Google Shared Folder and the writeup in class.
- (15) Do Homework Problem 8 (Duplicates and Three-Way Partition) from
Quickselect.
Instead of giving pseudocode in part (c), implement the ThreeWayPartition.java class from ThreeWayPartition.
Download that and the test program so you can test your implementation.
- (12) Do Homework Problem 8 (Greedy Coin Change) from Fractional Knapsack (Greedy).
Homework 14
- (10) Do the Huffman Encoding Bridges Assignment. Submit the code via you Google Shared Folder and the writeup in class.
- (10) Solve the instance of the 0-1 knapsack problem with
\(values=[8,6,7,5,3,9,3,10,3,8]\), \(weights=[3,5,3,2,1,3,3,1,2,3]\),
and knapsack weight \(W=12\). Show your table, and clearly trace back through
the table showing which items were chosen. Obviously also specify which
objects are taken (index the objects starting at 1)
and what the total value is.
- (10) Consider the following graph:
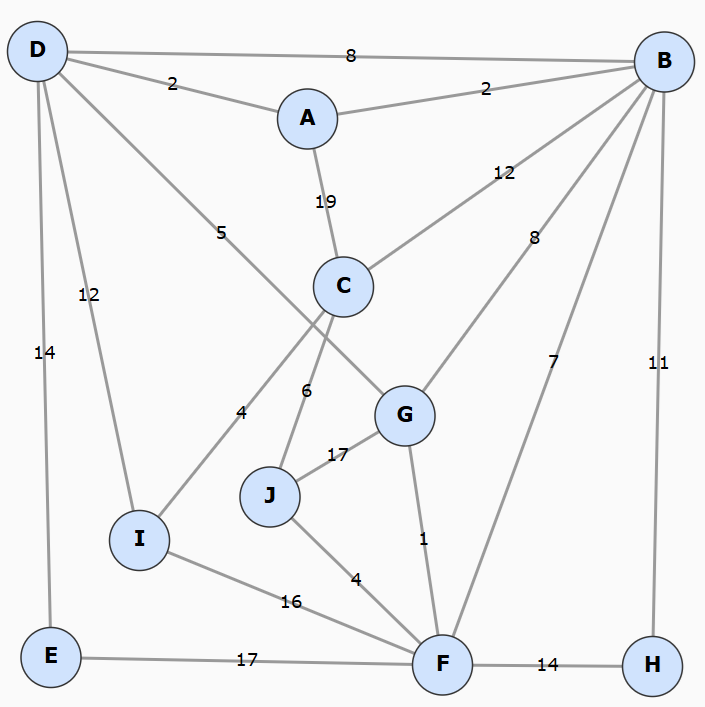
For both of the following problems, assume the graph is stored
using adjacency lists, and that all lists are stored in alphabetical order.
- Perform Prim's Algorithm on the graph.
Show the state of the priority queue at each step and
a table that gives for each vertex the key (min weight edge) and predecessor.
You do not have to make copies of the table--instead,
lightly cross off old values so I can see the history.
Make sure to give the final cost of the tree and darken the tree edges on the graph.
- Perform Kruskal's Algorithm on the graph.
List the edges in sorted order, and clearly indicate in order which are included
in the tree and which are not.
Make sure to give the final cost of the tree and darken the tree edges on the graph.
Homework 15
- (10) Do the BRIDGES Mountain Path Assignment.
Submit the code via you Google Shared Folder and the writeup in class.
- (10) Use Floyd's algorithm to find the solution to the all-pairs shortest path
problem for this graph whose adjacency matrix is given below.
Be sure to show the matrix at every step of the computation, mark the
relevant row/column of each, and highlight the cells that changed.
\[
\begin{bmatrix}
0 & 3 & 8 & \infty & 1 & \infty \\
\infty & 0 & \infty & 1 & 7 & \infty \\
\infty & 4 & 0 & \infty & \infty & 9 \\
2 & \infty & 2 & 0 & \infty & \infty \\
\infty & \infty & \infty & 6 & 0 & 3 \\
\infty & 10 & \infty & \infty & \infty & 0
\end{bmatrix}
\]
- (10) Consider the following array:
\([23, 87, 43, 21, 90, 54, 11, 74, 38, 41, 66, 32, 17]\).
Perform the following variation of Heap Sort on the array:
function heapSortVariation(A):
B = new heap; // Instead of buildHeap, do this:
for i from 0 to n-1: // Insert the elements from the array into
B.insert(A[i]) // the heap in order, one at a time.
for i from n-1 down to 1: // continue the second half as normal
swap B[0] with B[i] // move max to end
heapify(B, 0, i-1) // restore heap property
return B
Show the heap (drawn in tree form) at every step of insertion and deletion
(which happens as i decreases in the second loop).
As i decreases in the second loop, continue drawing the nodes, but disconnect nodes that are not logically in the heap anymore (the sorted elements).
Homework 16
- (10) Compute
\(13^{1303} \bmod 101\)
by hand using
- LTR Binary Exponentiation
- RTL Binary Exponentiation
Show all of your work (which should be a table with 3-5 columns for each computation).
You are permitted to verify that your answer is correct with the use of a computer or calculator.
In case it is not clear, you may do all of your intermediate computations modulo 101 and you will still get the same answer. For instance,
\(13*13=169=68 \bmod 101\), so you can use 68 instead of 169
in the next calculation.
- (20) Show all of the steps of inserting the letter of ALGORITHMS into each of the following data structures in order (e.g. A, then L, etc.)
- A regular (unbalanced) BST
- An AVL tree
- A Min Heap
- A Max Heap
Homework 17
- Consider the following problem:
Partition Problem.
Given a multiset S of positive integers, decide whether S can be split into two subsets with equal sum. An algorithm to solve
the problem should answer
yes or no, and provide the partition.
Example: If \(S=\{1, 3, 4, 7, 10, 23\}\), then the answer is yes
since \(S\) can be partitioned into \(\{1, 23\}\) and \(\{3, 4, 7, 10\}\),
each of which sums to 24.
- Give a very clear brute-force algorithm to solve the partition problem.
- Give the worst-case analysis of your brute-force algorithm.
- Give a very clear backtracking algorithm to solve the partition problem.
Do you have to do any precomputation before you start? Be clear on this.
- Give the backtracking tree for \(S = \{3, 5, 8, 10, 12, 14, 16\}\),
until you find a solution, and clearly state the solution.
- Given the set \(S=\{3, 7, 14, 22, 35, 41, 48, 56, 68, 77, 89, 94\}\),
compare how the two algorithms would perform.
For future: Monte-Carlo not ideal in this case-rewrite this part of the problem if using again.
- How many operations are needed for the brute-force algorithm?
-
Do three Monte-Carlo simulations to estimate the size of the
backtracking tree. That is, determine the size of each of the three trees,
and then average the sizes of the three to get an estimate of the average
tree size. Make sure to show all of your calculations.
- Given the size of the tree, estimate the number of operations necessary
to solve the problem
- Determine a fair way to compare the two calculations and comment on
the which algorithm seems to be better.
Homework 18Vibe Coding an Algorithm Demo
Goal: Create a demo of an algorithm (choices listed below) with the
assistance of your favorite AI tool(s). Make sure you do enough learning about your algorithm so you know that the demo is an accurate representation of how the algorithm works. Here are the details:
- Go to Books
- Right-click on the following files and download and save them somewhere (I will add the names below once assigned):
- Algorithm Demo TEMPLATE.html
- style.css
- demo.css
- demoScripts.js
- You will be assigned one of the following during an in-class discussion:
- Hashing--Open Addressing (insert, delete, search)
- Closest Pair (2D)--Brute Force (R-Dawg)
- Closest Pair (2D)--Divide-and-Conquer
- Unbalanced BST (insert, delete, search)
- 2-3 Trees (insert, delete, search) (Bryson)
- Red-Black Trees (insert, delete, search)
- AVL Trees (insert, delete, search) (Matthew)
- Fibonacci number using 2x2 matrix multiplication
- Dijkstra's Algorithm (Alem)
- Generating permutations
- Generating subsets (Wyatt)
- Give the 4 files to your favorite AI chatbot, describe the demo you want, dialog with it back and forth making sure it "understands" what you want.
- Tell it the demo should follow the template and use the style/js scripts and not override the style unless absolutely necessary
- Tell it the demo should use HTML/CSS/JS/SVG.
- Give it enough details about what the demo should display and what
the steps should do so it has a good starting point.
- If the algorithm is similar to one of the existing ones, download the existing demo code and feed it into the AI as a starting point.
- Submit the demo by copying the HTML file to your shard Google folder.
- You will also give a short presentation (10 minutes?) of your chosen algorithm, using the demo to explain the details.
Bonus! Write a page similar to those in DAIA to go along with your demo.
You will need to give the AI the following files as a starting point:
- Algorithm TEMPLATE.html
- style.css
- chapter.css
- chapterScripts.js
You can get an OK draft via AI, but getting a polished page involves a lot of back-and-forth with it to smooth everything out, make sure it makes sense and is readable, and make sure it is accurate.
|